The courses taught during the Ist semester can be seen here.

ELECTRONICS-I_2024-26

MATHEMATICAL PHYSICS - I_2024-26

                          The Course Outcomes (COs) of the course MP is given below, 

  • CO1 - Provide a solid foundation in Iinear algebra: This includes a thorough understanding of vectors, matrices, linear transformations, eigenvalues, eigenvectors, and the concept of diagonalization, Students will also learn the basics of tensor analysis.
  • CO2 - Understand infinite series and Fourier transforms: Students will be exposed to the concepts of infinite and power series, along with their convergence properties. Furthermore, they will learn about the Fourier series and Fourier transforms, including their properties and applications in physics.
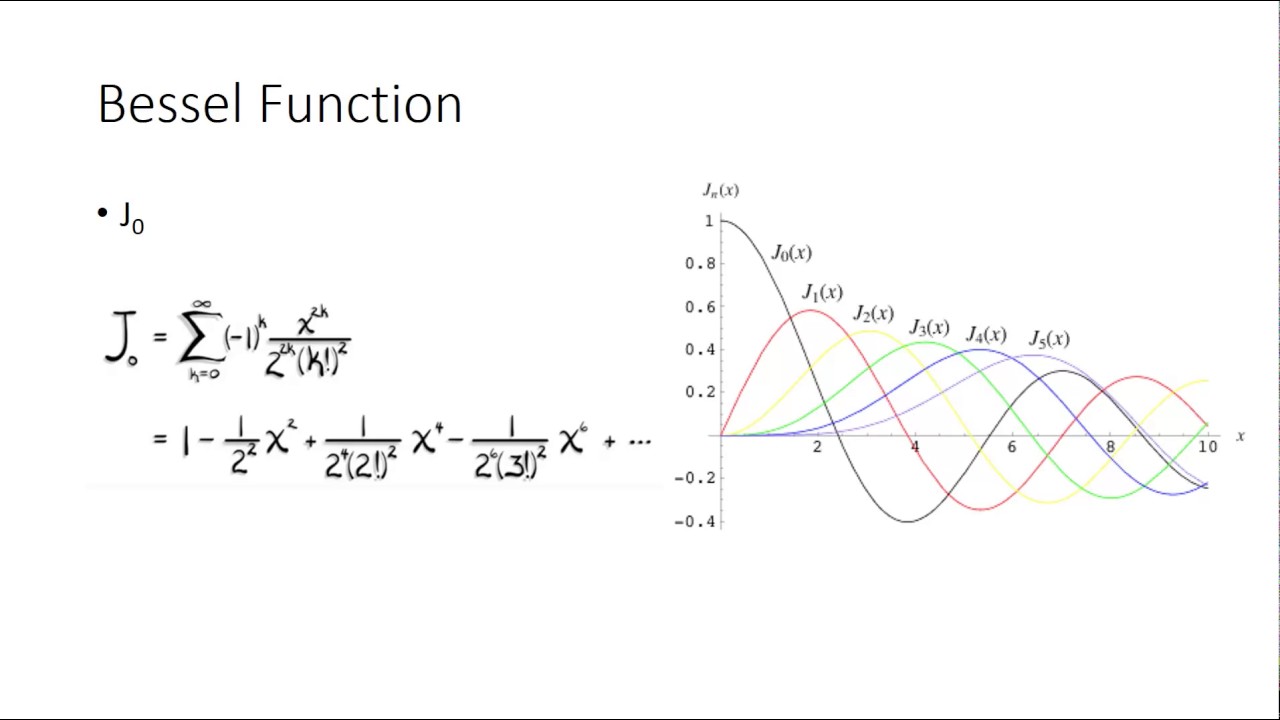
  • CO3 - Master special functions and orthogonal polynomials: The course aims to impart knowledge about special functions like Gamma and Beta functions, Legendre and Bessel functions, and the concept of orthogonal polynomials such as Hermite and Laguerre polynomials. Students will learn how these functions and polynomials are used to solve problems in physics.
  • CO4 - Develop expertise in ordinary and partial differential equations (ODEs and PDEs): Students will learn how to solve ODEs and pDEs, with a specific focus on systems of ODEs, the Laplace equation, and the wave equation. They will also gain an understanding of their applications in physics. 
  • CO5 - Apply mathematical methods to physical problems and promote computational skills: The course aims to develop students' ability to use these mathematical methods to analyse and solve problems in physics. The tutorial sessions will particularly focus on practical applications, enhancing problem-solving skills. As part of the course, students will use computational tools to solve complex problems, enhancing their computational physics skills

CLASSICAL MECHANICS_2024-26

                          The Course Outcomes (COs) of the CM course is given below,

  • Deal with particle mechanics at an advanced level.
  • Use the calculus of variations to characterize the function that extremizes a functional.
  • Understand the concept of constraints, principle of least action and formulation of Lagrange's method and apply Lagrange's equation for simple dynamical systems.
  • Understand Central force and its application in Kepler's problem.
  • Formulate and solve problems in classical mechanics using the Lagrangian, Hamiltonian and Hamilton-Jacobi formulations.
  • Apply the methods of classical mechanics to identify conserved quantities and normal modes.
  • Analyze motion of rigid bodies in non-inertial frames of reference using Euler angles and Euler's equations.